Enero

CENTRO DE MASA

Es el punto en el que se puede considerar está concentrada toda la masa de un cuerpo.

En equilibrio:

mag = mbg

ma = mb

1.-CASO DISCRETO 

(m1+m2)Xc = m1X1 + m2X2

Xc = m1X1+m2X2 / m1+m2

Yc = m1Y1+m2Y2 / m1+m2

Zc = m1Z1+m2Z2 / m1+m2

2.- CASO CONTNUO

 

                M = ∫dm

  

 DISTRIBUCIÓN DE MASA

i) DISTRINUCÍON LINEAL

λ = dm/dx [M/L]

λ = distribución lineal de masa

dm = diferencial de masa

dx = diferencial de longitud

Xc = ∫ xdm / ∫ dm = 1/M ∫ xdm  ; Yc = ∫ ydm / ∫ dm = 1/M ∫ ydm ; Zc = ∫ zdm / ∫ dm = 1/M ∫ zdm

ii) DISTRIBUCIÓN SUPERFICIAL

σ = dm/dA [M/L^2]

σ = distrinución superficial de masa

dA = diferencial de superfice

dm = σdA

iii) DISTRINUCIÓN VOLUMETRICA

δ = dm/dv [M/L^3]

δ = distrinución volumetrica de masa

dv = distrinución de volumen  

dm = δdv 

CAMPOS VECTORIALES

Definición de campo vectorial

Físicamente un campo vectorial representa la distribución espacial de una magnitud vectorial.

Matemáticamente se define un campo vectorial como una función vectorial de las coordenadas o como un caso especial de una transformación no necesariamente lineal. R^n=>R^m, en donde R^n representa el espacio vectorial que hace las veces de dominio y R^m el espacio vectorial que actúa como rango.

El campo ilustrado en la ecuación anterior es un campo vectorial R^3=>R^3, dado que la función vectorial tiene tres componentes y cada componente es una función de tres variables independientes.

Cuando se modela la distribución de esfuerzos en una estructura, la distribución de fuerzas de naturaleza electromagnética o gravitatoria en el espacio, se hace usando campos vectoriales.

Otros ejemplos de campos vectoriales son las funciones de velocidad asociadas a las trayectorias de las partículas o diferenciales de volumen de una sustancia en condiciones de flujo bien sea laminar o turbulento.

Representación de un campo vectorial

Líneas de fuerza

La representación de los campos vectoriales se hace mediante mapas semejantes a los de los campos escalares, pero usando líneas que representan la continuidad de la orientación de los vectores de campo sobre una región definida. Estas líneas reciben el nombre de líneas de fuerza.

Al igual que con los campos escalares, un campo vectorial no puede representarse fácilmente en tres dimensiones, por lo que normalmente se hacen proyecciones sobre los planos directores del sistema de coordenadas.

Las líneas de fuerza cumplen con las siguientes propiedades:

• Los vectores de campo en cualquier punto son siempre tangenciales a la línea de fuerza que pasa por el punto dado.
• Las líneas de fuerza no se cruzan en ningún punto aunque pueden seguir trayectorias cerradas.
• La cantidad de líneas de fuerza en cualquier porción del espacio en que se encuentra definido el campo es proporcional a la intensidad del campo vectorial.

En algunas otras ocasiones, la representación de campos vectoriales se hace a través de los vectores de campo directamente. En estos casos, la intensidad del campo vectorial se asocia a la densidad de vectores de campo en una región, tanto como a la longitud de los mismos.

Rotacional y Divergencia

Rotacional

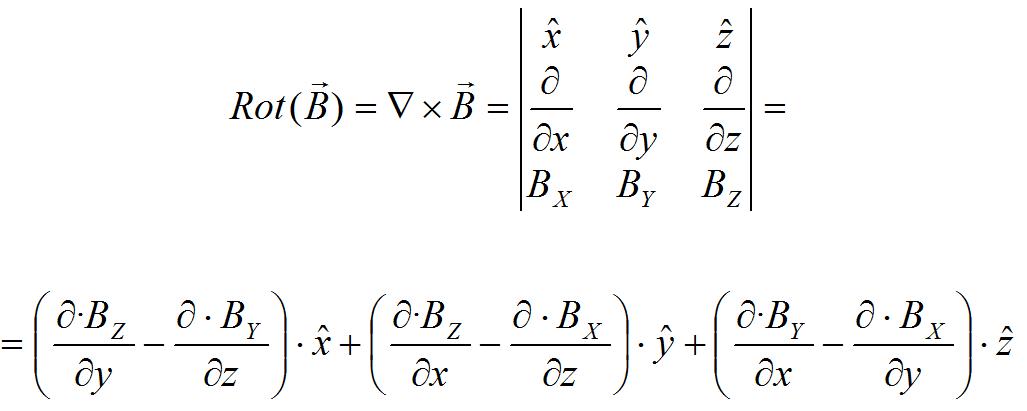
Se entiende por rotacional al operador vectorial que muestra la tendencia de un campo a inducir rotación alrededor de un punto. También se define como la circulación del vector sobre un camino cerrado del borde de un área con dirección normal a ella misma cuando el área tiende a cero . 

Aquí, /\s es el área de la superficie apoyada en la curva C , que se reduce a un punto. El resultado de este límite no es el rotacional completo (que es un vector), sino solo su componente según la dirección normal a /\s y orientada según la regla de la mano derecha. Para obtener el rotacional completo deberán calcularse tres límites, considerando tres curvas situadas en planos perpendiculares.

El rotacional de un campo se puede calcular siempre y cuando este sea continuo y diferenciable en todos sus puntos.

El resultado del rotacional es otro campo vectorial que viene dado por el determinante de la siguiente ecuación:

Las propiedades más destacadas del rotacional de un campo son:

•  Si el campo escalar f(x,y,z) tiene derivadas parciales continuas de segundo orden entonces el rot (\/f) =0

•  Si F(x,y,z) es un campo vectorial conservativo entonces rot (F) = 0

•  Si el campo vectorial F(x,y,z) es una función definida sobre todo R^3 cuyas componentes tienen derivadas parciales continuas y el rot (F) = 0, entonces F es un campo vectorial conservativo.

Divergencia

La divergencia de un campo vectorial mide la diferencia entre el flujo entrante y el flujo saliente en una superficie que encierra un elemento de volumen dV . Si el volumen elegido solamente contiene fuentes o sumideros de un campo, entonces su divergencia es siempre distinta de cero.

La divergencia de un campo vectorial en un punto es un campo escalar, que se define como el flujo del campo vectorial por unidad de volumen conforme el volumen alrededor del punto tiende a cero, para el caso del campo magnético la divergencia viene dada por la ecuación donde S es una superficie cerrada que se reduce a un punto en el límite, B es el campo magnético, V es el volumen que encierra dicha superficie S y \/ es el operador nabla, que se calcula de la siguiente forma:

La divergencia de un campo es un valor escalar con signo. Si este signo es positivo, quiere decir que el campo emana hacia el exterior de dicho punto y, por tanto, es una fuente o manantial. Si el signo es negativo, el campo converge hacia un punto del interior del volumen, por lo que constituiría un sumidero. 

Si la divergencia fuese cero el campo neto (diferencia entre las líneas entrantes y salientes) sería nulo.

En el caso de los campos magnéticos se ha comprobado la ausencia de fuentes y/o sumideros de ahí que una de sus propiedades sea que su divergencia es nula 

Los campos cuya divergencia es cero se denominan campos solenoidales, que se caracterizan porque sus líneas de campo son cerradas sobre si mismas, es decir, no tienen extremos donde nacen o mueren. De tener dichos extremos, el flujo neto alrededor de uno de ellos no sería nulo, lo cual denotaría la existencia de una fuente o sumidero del campo.